Question

The famous cliff divers of Acapulco leap from a perch 35 m above the ocean. How fast are they moving when they reach the surface? What happens to their kinetic energy as they slow to a stop in the water? Please show how you get the energy conservation equation

Answer 1

1) 26.2 m/s

The mechanical energy of the divers at any point of their vertical motion is sum of the kinetic energy and the gravitational potential energy:

`E=K+U = (1)/(2)mv^2 + mgh`

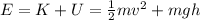
where

m is the mass of the diver

v is the speed

g = 9.8 m/s^2 is the acceleration due to gravity

h is the height above the water

When the diver is on the cliff, v = 0 (he is at rest), so K=0 and the initial mechanical energy is just potential energy:

`E_i = mgh`

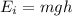
where h=35 m is the height of the cliff.

When the diver hits the water above, h = 0, so U=0 and the final mechanical energy is just kinetic energy:

`E_f = (1)/(2)mv^2`

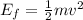
since the total mechanical energy is conserved, we have

`E_i = E_f\\mgh = (1)/(2)mv^2`

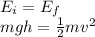
And solving the equation for v, we find the speed when they reach the surface of the water:

`v=√(2gh)=√(2(9.8 m/s^2)(35 m))=26.2 m/s`

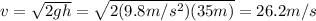
2) It is converted into thermal energy of the water

When the diver enters the water, he suddenly feels another force acting against the motion of the diver: the resistance of the water. The resistance of the water acts upward, slowing down the diver until he stops.

In this process, the speed of the diver (v) decreases, and therefore the kinetic energy of the diver decreases as well, until it becomes zero.

However, this does not mean that the conservation of energy has been violated. In fact, the kinetic energy of the diver has been converted into thermal energy of the molecules of water surrounding the diver.