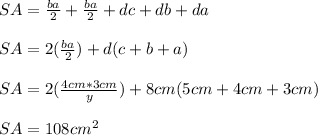Answer: Option C.
Explanation:
The surface area of the right triangular will be the sum of all its faces.
You can observe in the figure that the faces of the right triangular prism are: Two equal right triangles and three different rectangles.
The formula for calculate the area of a triangle is:

Where "b" is the base and "h" is the height.
The formula for calculate the area of a rectangle is:
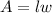
Where "l" is the length and "w" is the width.
Then, the surface area of the right triangular prism is: