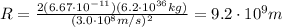A)
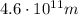
The period of the orbit of the clumps around the black hole is
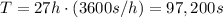
While their orbital speed is
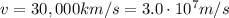
And the orbital speed is equal to the ratio between the circumference of the orbit and the orbital period:

So re-arranging the equation, we find the radius of the orbit of the clumps:
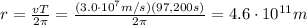
B)
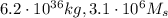
The mass of the black hole can be found by equalizing the gravitational attraction between the black hole and the clumps to the centripetal force:
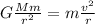
where G is the gravitational constant, M the mass of the black hole, m the mass of the clumps.
Solving for M,
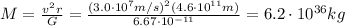
And since 1 solar mass is
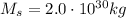
the mass of the black hole in multuple of solar masses is
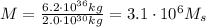
C)
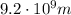
The radius of the event horizon of a black hole is given by
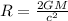
where
G is the gravitational constant
M is the mass of the black hole
c is the speed of light
Substituting, we find