Question

1) If a pendulum clock keeps perfect time at the base of a mountain, will it also keep perfect time when it is moved to the top of the mountain? Explain.

2)if a grandfather clock is running slow, how could we adjust the length of the pendulum to correct the time?
3)Explain (a) how it is possible for a large force to produce only a small, or even zero, torque, and (b) how it is possible for a small force to produce a large torque.

Answer 1

1) No

Step-by-step explanation:

The period of a pendulum is given by

`T=2\pi \sqrt{(L)/(g)}`

where

L is the length of the pendulum

g is the acceleration due to gravity

The value of g, acceleration due to gravity, is not exactly the same in all locations of the Earth. In fact, its value is given by

`g=(GM)/(r^2)`

where G is the gravitational constant, M is the Earth's mass, and r the distance of the point from the Earth's center. This means that at the top of a mountain, r is slightly larger than at the Earth's surface, so the value of g is slightly smaller at the top of the mountain, and therefore the period of the pendulum will also be different (it will be slightly longer than at Earth's surface).

2) We need to decrease the length of the pendulum

Again, the period is given by

`T=2\pi \sqrt{(L)/(g)}` (1)

If the clock is running slow, it means that its period T' is slightly longer than the expected period T: so, we need to shorten the period.

From eq.(1), we see that the period is proportional to the square root of the length of the pendulum, L: therefore, if the length increases the period increases, and if the length decreases, the period will decreases.

Here we want to shorten the period: therefore, according to the equation, we need to decrease the length of the pendulum.

3)

The torque of a force applied is given by

`\tau = Fd sin \theta`

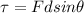
where

F is the magnitude of the force

d is the distance between the point of application of the force and the pivot point

`\theta` is the angle between the direction of the force and d

So we have:

a) If we have a large force F, it is possible to produce a small torque by decreasing d, so by applying the force really close to the pivot, or by decreasing
`\theta`, which means applying the force as more parallel as possible to d. The torque will be even zero if d=0 (force applied at the pivot point) or if
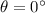`\theta=0^(\circ)` (force parallel to d)

b) if we have a small force F, it is possible to produce a large torque by increasing d, so by applying the force really far to the pivot, or by increasing
`\theta`, which means applying the force as more perpendicular as possible to d.