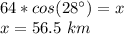Answer:

Explanation:
Given the right triangle in the image, you need to remember the following identity:
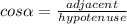
Observe the triangle. You can identify that:
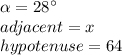
Then, knowing these values, you can substitute them into
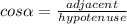 :
:
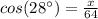
Finally, you have to solve for "x".
Therefore, the value of "x" rounded to the nearest tenth is: