Answer:
D.

Explanation:
In the polynomial
 group first two terms and second two terms:
group first two terms and second two terms:

First two terms have common factor
 and last two terms have common factor
and last two terms have common factor
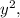 hence
hence
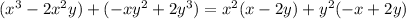
In brackets you can see similar expressions that differ by sign, so
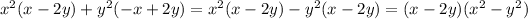
Now use formula
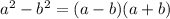
You get
