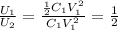Answer:
1/2
Step-by-step explanation:
The energy stored in a capacitor is given by
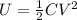
where
C is the capacitance
V is the potential difference
Calling
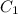 the capacitance of capacitor 1 and
the capacitance of capacitor 1 and
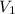 its potential difference, the energy stored in capacitor 1 is
its potential difference, the energy stored in capacitor 1 is
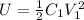
For capacitor 2, we have:
- The capacitance is half that of capacitor 1:
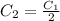
- The voltage is twice the voltage of capacitor 1:
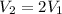
so the energy stored in capacitor 2 is
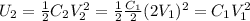
So the ratio between the two energies is