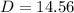Answer:
Explanation:
We know that the diameter of a circle is twice the radius.
Calculate the radius of the circle with the formula for calculate the distance between two points:
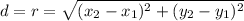
Where "r" is the radius.
Knowing that the center of the circle is at point (3, 1) and the circle passes through the point (1, -6), we can substitute values into the formula to find the radius:

Then the diameter of the circle is: