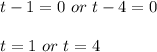Answer:
Explanation:
Given that:
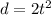 and
and

If we equate both since they are distances, we have:
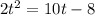
Algebraically, moving the equation to the right side, we get:
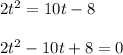
To factor the equation on the left side:

Factor out 2 on the left-hand side:
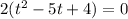
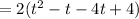
![= 2[t(t-1)-4(t-1)]](https://img.qammunity.org/2022/formulas/mathematics/college/d4qw7603kd46035fff4hri4o8bdwe3kopy.png)
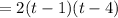
To determine the time when the two boats have to cover an equal distance:
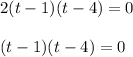
Thus: