Answer:
Is not a function
Explanation:
A relation is a function if each value of the input set (domain) is assigned only one value of the output set (range)
Given a function
 , the inverse of f denoted
, the inverse of f denoted
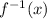 is a function only if f(x) is a one-to-one function. This means that there are not in the domain of
is a function only if f(x) is a one-to-one function. This means that there are not in the domain of
 two distinct values of x that produce the same value of y.
two distinct values of x that produce the same value of y.
In the graph of f(x) you can see that the function is not one-to-one. Since
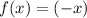 for all x.
for all x.
For example:
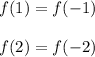
Observe the attached graph
In general, the inverse of a quadratic function f(x) is not a function