Question

A car traveling along the highway needs a certain amount of force exerted on it to stop it in a

certain distance. More stopping force is required when the car has
A) more mass.
B) more momentum.
C) less stopping distance.
D) all of these
E) none of these

Answer 1

A car traveling along the highway needs a certain amount of force exerted on it to stop it in a certain distance.

More stopping force is required when the car has more mass, or more momentum, or less stopping distance. (D)

Answer 2

More stopping force is required when the car has D) all of these.

Step-by-step explanation:

Let's explain some equations and concepts in order to answer the question:

• The second law of Newton states that a force exerted on an object is directly proportional to the mass of the object and the acceleration of the object.

• Mathematically, we can write the following equation :

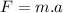`F=m.a` (I)

Where ''F'' is the force

Where ''m'' is the mass

And where ''a'' is the acceleration.

Now, we can define the momentum as :

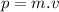`p=m.v` (II)

The momentum ''p'' is a vector magnitude.

''m'' is the mass of the object

And ''v'' is the velocity vector.

Finally, let's explain the following motion equation :

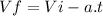`Vf=Vi-a.t` (III)

Vf is final speed

Vi is initial speed

''a'' is the acceleration of the object.

Notice that we write a ''-'' in the ''a.t'' term because we assume that the object is stopping. Therefore, its acceleration is negative. ''t'' is the time in which the object will stop.

Let's proceed analyzing each option :

• A) more mass

If the car has more mass, therefore by looking at the equation (I), the stopping force will be greater.

• B) more momentum

By looking the equation (II), if the car has more momentum therefore it has more mass or more speed (or both).

If it has more mass the stopping force required must be greater.

Otherwise, if it has more speed, by looking at the equation (III) and assuming that Vf = 0 (because we need the car to stop) ⇒

`0=Vi-a.t`

`Vi=a.t`

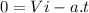
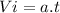
If
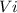`Vi` is greater and assuming that time must be the same, therefore the acceleration will be greater. So, if acceleration increases, the stopping force increases (looking at equation (I) ).

• Finally, C) less stopping distance

If the car has less stopping distance, therefore the magnitude of the acceleration vector must be greater (in order to stop the car faster). By looking the equation (I) we conclude that the stopping force will be greater.

The correct option is D) all of these