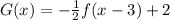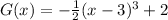Answer:
The equation is
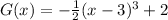
Explanation:
If the graph of the function
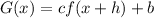 represents the transformations made to the graph of
represents the transformations made to the graph of
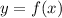 then, by definition:
then, by definition:
If
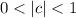 then the graph is compressed vertically by a factor c.
then the graph is compressed vertically by a factor c.
If
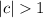 then the graph is stretched vertically by a factor c
then the graph is stretched vertically by a factor c
If
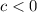 then the graph is reflected on the x axis.
then the graph is reflected on the x axis.
If
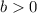 the graph moves vertically upwards.
the graph moves vertically upwards.
If
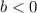 the graph moves vertically down
the graph moves vertically down
If
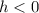 the graph moves horizontally h units to the right
the graph moves horizontally h units to the right
If
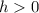 the graph moves horizontally h units to the left
the graph moves horizontally h units to the left
In this problem we have the function
 and our parent function is
and our parent function is
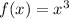
We know that G(x) is equal to f(x) but reflected on the x-axis (
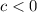 ), compressed vertically by a multiple of 1/2 (
), compressed vertically by a multiple of 1/2 (
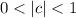 and
and
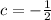 ), displaced 2 units upwards (
), displaced 2 units upwards (
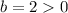 ) and moved to the right 3 units (
) and moved to the right 3 units (
 )
)
Then: