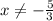Question

Given: f(x) = x + 2 and g(x) = 3x + 5
f (x)/g (x) =

Answer 1

`(f(x))/(g(x))=(x+2)/(3x+5)`

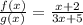
where
`x\\e -(5)/(3)`

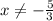
Explanation:

The given functions are:

f(x) = x + 2 and g(x) = 3x + 5

`(f(x))/(g(x))=(x+2)/(3x+5)`

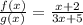
Since this is a rational function, the function will not be defined where denominator equals zero.

We need to restrict the function or define the domain.

This is a rational function defined for
`x\\e -(5)/(3)`

Answer 2

For this case we have two functions of the form y = f (x). We must find the quotient of the following functions:

`f (x) = x + 2\\g (x) = 3x + 5`

So, we have by definition:

`\frac {f (x)} {g (x)} = \frac {x + 2} {3x + 5}`

Answer:

`\frac {f (x)} {g (x)} = \frac {x + 2} {3x + 5}`

with 3x + 5 different from zero, so that the function is defined