Question

Please help!

In circle Y, what is m?


82°

100°

106°

118°

Answer 1

The correct option is: 82°

Explanation:

In the given diagram, two chords
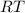`RT` and
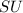`SU` are intersecting.

According to the Angle of intersecting chord theorem, "If two chords intersect inside a circle, then the measure of the angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle."

That means here......

`94\°=(1)/(2)(m\widehat{RS}+m\widehat{TU})\\ \\ 94\°=(1)/(2)(106\°+m\widehat{TU})\\ \\ 2(94\°)=106\°+m\widehat{TU}\\ \\ 188\°=106\°+m\widehat{TU}\\ \\ m\widehat{TU}=188\°-106\°=82\°`

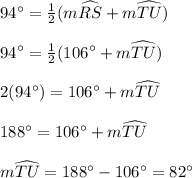
So, the measure of arc
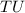`TU` is 82°