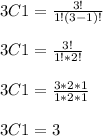Question

Evaluate 3C1.

a)3
b)1
c)2
d)6

Answer 1

Answer: Option a) 3

Explanation:

The formula for calculating combinations is as follows

`nCr = (n!)/(r!(n-r)!)`

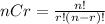
Where "n" is the amount of items in a set and you can choose "r" from them

3C1 reads as: The combination of 1 in 3. You have a set of 3 elements and choose 1 of them.

`n = 3\\\\r = 1`

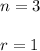
So :

`3C1=(3!)/(1!(3-1)!)\\\\3C1=(3!)/(1!*2!)\\\\3C1=(3*2*1)/(1*2*1)\\\\3C1=3`