Question

Which row function are inverses of each other?

Answer 1

Third Option

`f(x) = 4x,\ g(x)=(1)/(4)x`

Explanation:

For a function f(x) it is satisfied that the range of f(x) is equal to the domain of its inverse function. In the same way the domain of f(x) is equal to the range of its inverse.

Therefore, to verify which pair of functions are inverse to each other, perform the composition of both functions and you must obtain

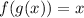`f(g(x)) = x` and
`g(f(x)) = x`

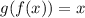
For the first option we have:

`f(x) = x,\ g(x)=-x`

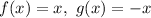
Then

`f(g(x)) = (-x) = -x` They are not inverse functions

For the second option we have:

`f(x) = 2x,\ g(x)=-(1)/(2)x`

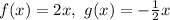
Then

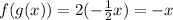`f(g(x)) = 2(-(1)/(2)x) = -x` They are not inverse functions

For the third option we have:

`f(x) = 4x,\ g(x)=(1)/(4)x`

Then

`f(g(x)) = 4((1)/(4)x) = x`

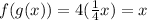
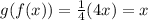`g(f(x)) = (1)/(4)(4x) = x` They are inverse functions

For the fourth option we have:

`f(x) = -8x,\ g(x)=8x`

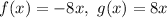
Then

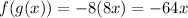`f(g(x)) = -8(8x) = -64x` They are not inverse functions