The width of the outer edge of each piece of cake 8.4 inches.
SOLUTION:
Given, a circular cake with a radius of 8 inches is cut from the center into 6 equal pieces. We have to find the width of the outer edge of each piece of cake.
We know that the circumference of a circle can be calculated with this formula:
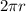 where "r" is the radius of the circle.
where "r" is the radius of the circle.
We know that the circular cake (whose radius is 8 inches) is cut from the center into 6 equal pieces.
Then, you need to divide the circumference of this circular cake by 6 to find the width of the outer edge of each piece of cake.
Therefore, this is (to the nearest tenth of an inch):
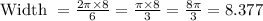
Hence, the cake piece is 8.4 inches wide.