Answer: Option B
2 is NOT in the domain of f ° g
Explanation:
First we must perform the composition of both functions:
If
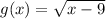 and not
and not
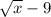
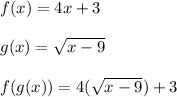
The domain of the composite function will be all real numbers for which the term that is inside the root is greater than zero. When x equals 2, the expression within the root is less than zero
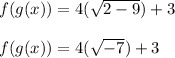
The root of -7 does not exist in real numbers, therefore 2 does not belong to the domain of f ° g
The answer is Option B.
Note. If
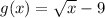
So
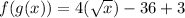 And 2 belongs to the domain of the function
And 2 belongs to the domain of the function