Question

(X-2) is a factor of x^4+2x^3-7x^2-8x+12. The other factors are ____, ____, and _____

Answer 1

We have

`(x^4+2x^3-7x^2-8x+12)/(x-2)=x^3+4x^2+x-6`

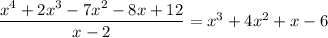
The rational root theorem suggests that other possible roots may be -6, 6, -3, 3, -2, 2, -1, and 1. It turns out that
`x=-2` is a root, since
`(-2)^3+4(-2)^2+(-2)-6=0`, so
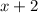`x+2` is also a factor and we have

`(x^4+2x^3-7x^2-8x+12)/((x-2)(x+2))=x^2+2x-3`

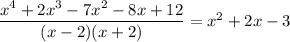
Finally, we can factorize the remaining quotient easily:

`x^2+2x-3=(x+3)(x-1)`

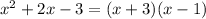
so the other factors are
`x+2`,
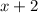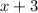`x+3`, and
`x-1`.