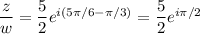Question

Let z= -5 sqrt 3/2 + 5/2i and w=1 + sqrt 3i

a. Convert z and w to polar form.

b. Calculate zw using De Moivre’s Theorem.

c. Calculate (z / w) using De Moivre’s Theorem.

Answer 1

a.

`z=-\frac{5\sqrt3}2+\frac52i=5\left(-\frac{\sqrt3}2+\frac12i\right)=5e^(i5\pi/6)`

`w=1+\sqrt3\,i=2\left(\frac12+\frac{\sqrt3}2i\right)=2e^(i\pi/3)`

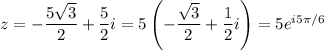
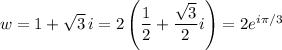
b. Not exactly sure how DeMoivre's theorem is relevant, since it has to do with taking powers of complex numbers... At any rate, multiplying
`z` and
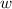`w` is as simple as multiplying the moduli and adding the arguments:

`zw=5\cdot2e^(i(5\pi/6+\pi/3))=10e^(i7\pi/6)`

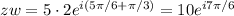
c. Similar to (b), except now you divide the moduli and subtract the arguments:

`\frac zw=\frac52e^(i(5\pi/6-\pi/3))=\frac52e^(i\pi/2)`