Question

Simplify the complex fraction

((3x-7)/x^2)/(x^2/2)+(2/x)

I really need steps on how to do this properly cause I really can't figure it out

Answer 1

`(6x-14)/(x^(4) +4x)`

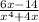
Explanation:

I have to
`((3x-7)/(x^(2) ) )/((x^(2) )/(2)+(2)/(x))`

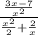
Let's start by joining the macro denominator with a common denominator. So, by applying a minimum common multiple
`(x^(2) )/(2) +(2)/(x)=(x^(3)+ 4 )/(2x)`

Now I can write the expression as

`((3x-7)/(x^(2)))/((x^(3)+ 4 )/(2x))`

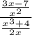
Now to convert both fractions into one, I multiply the numerator of the one above by the denominator of the one below, and the denominator of the one above with the numerator below, remaining that way.

`((3x-7)/(x^(2)))/((x^(3)+4)/(2x))=((3x-7)(2x))/((x^(2))(x^(3)+ 4))`

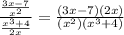
Having the fraction in this way, I could simplify the x of the "2x" of the numerator with an x^2 (x^2=x*x) of the denominator

`((3x-7)(2x))/((x^(2))(x^(3)+4))=(2(3x-7))/(x(x^(3)+ 4))`

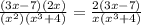
finally, applying distributive property, I have to

`((6x-14))/((x^(4)+ 4x))`

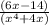
Done