Question

Which expression represents the distance between point (0,a) and point (a,0) on a coordinate grid?

Answer 1

You can always compute the distance between two points
`(x_1,y_1)` and
`(x_2,y_2)` using the pythagorean theorem:

`d = √((x_1-x_2)^2+(y_1-y_2)^2)`

In your case, we have

`d = √((0-a)^2+(a-0)^2) = √(2a^2)=a√(2)`

Answer 2

`√(2)a`

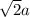
Explanation:

We are asked to find the distance between point (0,a) and point (a,0) on a coordinate grid.

We will use distance formula to solve our given problem.

The distance between two points
`(x_1,y_1)` and
`(x_2,y_2)` is given by formula:

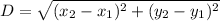`D=√((x_2-x_1)^2+(y_2-y_1)^2)`, where D represents distance between two points.

Let point
`(0,a)=(x_1,y_1)` and point
`(a,0)=(x_2,y_2)`.

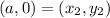Substitute the values in distance formula:

`D=√((0-a)^2+(a-0)^2)`

`D=√((-a)^2+(a)^2)`

`D=√(a^2+a^2)`

`D=√(2a^2)`

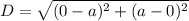
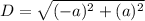
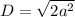
Factor out perfect square:

`D=√(2)a`

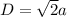
Therefore, the distance between two points would be
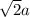`√(2)a`.