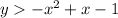Question

Which inequality statement best represents the graph?

f(x) > –x2 + x – 1

f(x) < x2 + x – 1

f(x) < –x2 + x – 1

f(x) > x2 + x – 1

Answer 1

f(x) < –x2 + x – 1

Explanation:

The graph is going down so we know that there is a maximum, therefore the A value has to be negative. This rules out f(x) < x2 + x – 1 and f(x) > x2 + x – 1 . The shaded area of the graph is below which indicates that f(x) has to be less than the function. This means the correct answer is f(x) < –x2 + x – 1 .

Answer 2

`y>-x^2 +x-1`

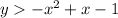
Explanation:

Lets find the inequality that best describes the given statement

The graph of the parabola is upside down so the value of 'a' is -1

It means the equation for the parabola becomes
`y=-x^2 +x-1`

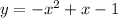
Now to get inequality , lets pick a point from the shaded part .

Lets pick (0,0), plug in 0 for x and 0 for y

`y=-x^2 +x-1`

`0=-(0)^2 +(0)-1`

`0=-1`

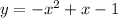
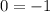
0 is greater than -1

`y>-x^2 +x-1`