Question

Simplify the complex fraction

((3x-7)/x^2)/(x^2/2)+(2/x)

I really need steps on how to do this properly cause I really can't figure it out
`((3x-7)/(x^2) )/((x^2)/(2)+ (2)/(x) )`

Answer 1

The simplest form is 2(3x - 7)/x(x³ + 4)

Explanation:

* Lets revise how can divide fraction by fraction

- To simplify (a/b)/(c/d), change it to (a/b) ÷ (c/d)

∵ a/b ÷ c/d

- To solve it change the division sign to multiplication sign and

reciprocal the fraction after the sign

∴ a/b × d/c = ad/bc

* Now lets solve the problem

∵
`((3x-7)/(x^(2)))/((x^(2))/(2)+(2)/(x))`

- Lets take the denominator and simplify by make it a single

fraction, let the denominator of it 2x and change

the numerator

∴
`(x^(2))/(2)+(2)/(x)=(x(x^(2))+2(2))/((2)(x))=(x^(3)+4)/(2x)`

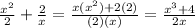
∴ The fraction =
`((3x-7)/(x^(2)))/((x^(3)+4)/(2x))`

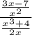
* Now lets change it by (up ÷ down)

∴
`(3x-7)/(x^(2))` ÷
`(x^(3)+4)/(2x)`

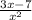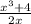
- Change the division sign to multiplication sign and reciprocal

the fraction after the sign

∴
`(3x-7)/(x^(2))` ×
`(2x)/(x^(3)+4)`

∴
`((2x)(3x-7))/((x^(2))(x^(3)+4))`

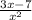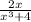
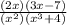
- We can simplify x up with x down

∴
`(2(3x-7))/(x(x^(3)+4))`

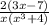
* The simplest form is 2(3x - 7)/x(x³ + 4)