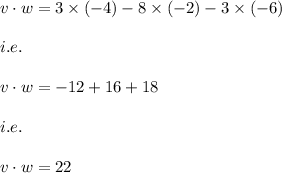Question

Can someone please help me out with this question? I need an answer ASAP. Thank you!!!

Evaluate the expression:


v ⋅ w


Given the vectors:


r = <8, 8, -6>; v = <3, -8, -3>; w = <-4, -2, -6>

Answer 1

Multiply corresponding components, then add the products:

`v\cdot w=3(-4)+(-8)(-2)+(-3)(-6)=22`

Answer 2

The resultant of the dot product of two vectors is:

`v\cdot w=22`

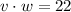
Explanation:

We are asked to find the dot product of the two vectors v and w.

The vectors are given by:

r = <8, 8, -6>; v = <3, -8, -3>; w = <-4, -2, -6>

This means that in the vector form they could be written as follows:

`r=8\hat i+8\hat j -6\hat k\\\\v=3\hat i-8\hat j -3\hat k\\\\w=-4\hat i-2\hat j -6\hat k`

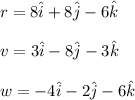
Hence, the dot product of two vectors is the sum of the product of the entries corresponding to each direction component.

i.e. the x-component get multiplied to each other, y-component get multiplied to each other and so happens with z.

Hence, the dot product of v and w is calculated as:

`v\cdot w=3* (-4)-8* (-2)-3* (-6)\\\\i.e.\\\\v\cdot w=-12+16+18\\\\i.e.\\\\v\cdot w=22`