 has degree 3, so it takes the general form
has degree 3, so it takes the general form
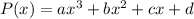
It has a root
 of multiplicity 2, which means
of multiplicity 2, which means
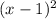 divides
divides
 exactly, and it has a root of
exactly, and it has a root of
 of multiplicity 1 so that
of multiplicity 1 so that
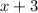 also is a factor. So
also is a factor. So

Expanding this gives
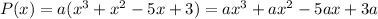
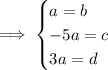
The
 -intercept occurs for
-intercept occurs for
 , for which we have
, for which we have

Then
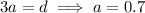

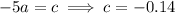
So we have
