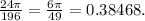Question

A target with a diameter of 14cm has 4 scoring zones by concentric circles. The diameter of the center circle is 2 cm. The width of each ring is 2 cm. A dart hits the target at a random point. Find the probability that it will hit a point in the outer (yellow) ring

Answer 1

0.38468

Explanation:

To know the probability we need to know the area of the yellow zone and the area of the rest. So, the yellow circle (that contains white, red and blue circle) has a radius of 1+2+2+2=7. Then the area is

Area yellow=
`\pi r^(2)= \pi *7^(2)=49\pi.`

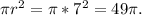
But, the yellow zone is yellow circle - blue circle.

Area blue =
`\pi r^(2)= \pi *(1+2+2)^(2)=\pi *5^(2)=25\pi.`

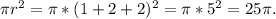
Then, the yellow zone will be
`49\pi-25\pi=24\pi.`

Area target= 14*14 = 196.

So, the probability is the yellow zone divided by the target (total area):

P =
`(24\pi)/(196)= (6\pi)/(49)= 0.38468.`

Answer 2

`48.98\%`

Explanation:

we know that

The probability that it will hit a point in the outer (yellow) ring is equal to divide the area of the yellow ring by the total area of the target

step 1

Find the area of the yellow ring

`A=\pi [7^(2) -5^(2)]`

`A=24\pi\ cm^(2)`

step 2

Find the total area of the target

`A=\pi [7^(2)]`

`A=49\pi\ cm^(2)`

step 3

Find the probability

`24\pi/49\pi=0.4898`

Convert to percentage

`0.4898*100=48.98\%`