Question

State if the triangles in each pair are similar.

If so, state how you know they are similar and complete the similarity statement.
A) similar; SAS similarity; ΔBAC
B) not similar
C) similar; SSS similarity; ΔABC
D) similar; SAS similarity; ΔABC

Answer 1

Option C) similar; SSS similarity; ΔABC

Explanation:

we know that

The SSS similarity state : If the corresponding sides of two triangles are proportional, then the two triangles are similar

In this problem

80/30=56/21=72/27

2.67=2.67=2.67 -----> is true

therefore

The triangles STU and ABC are similar by SSS similarity

Answer 2

Answer: The correct option is

(C) similar; SSS similarity; ΔABC.

Step-by-step explanation: We are given to check whether the pair of triangles in the figure are similar to each other or not.

If so, we are to complete the similarity statement.

From the figure, we note that

the lengths of the sides of triangle STU are

ST = 72, TU = 80 and SU = 56.

And, the lengths of the sides of triangle ABC are

AB = 27, BC = 30 and AC = 21.

So, we get

`(ST)/(AB)=(72)/(27)=(8)/(3),\\\\\\(TU)/(BC)=(80)/(30)=(8)/(3),\\\\\\(SU)/(AC)=(56)/(21)=(8)/(3).`

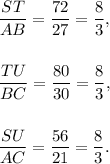
That is,

`(ST)/(AB)=(TU)/(BC)=(SU)/(AC)=(8)/(3).`

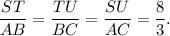
Therefore, the corresponding sides of the two triangles are proportional.

Hence, triangle ABC and STU are similar by SSS similarity.

Option (C) is CORRECT.