Question

Which statement correctly compares the slopes of the two functions?

Answer 1

The statement which correctly compares the slopes of two functions is:

• Function f(x) has a slope 2, which makes is steeper than g(x)

Explanation:

If the slope of a function has a greater absolute value as compared to other then that function is steeper than the other.

Here we have a function f(x) as:

`3x-y=6`

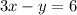
On changing to slope-intercept form of a line

i.e. y=mx+c

where m is the slope of the line and c is the y-intercept of the line we have:

`f(x)=y=3x-6`

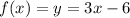
i.e. the slope of function f(x) is: 3

The function g(x) is a graph that passes through (-2,1) and (-1,3)

The equation for y=g(x) is given by:

`y-1=(3-1)/(-1-(-2))* (x-(-2))\\\\\\y-1=(2)/(-1+2)* (x+2)\\\\\\i.e.\\\\\\y-1=(2)/(1)* (x+2)\\\\\\i.e.\\\\\\y=2x+4+1\\\\\\i.e.\\\\\\y=2x+5`

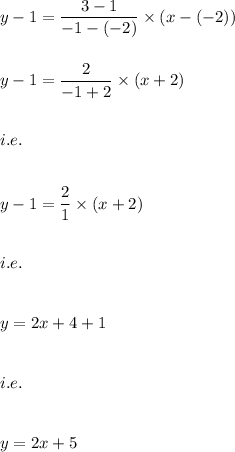
( since we used a concept of a line passing through two-point (a,b) and (c,d) is given by the equation:

`y-b=(d-b)/(c-a)* (x-a)` )

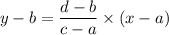Hence, the slope of function g(x) is: 2

The absolute value of slope of function f(x) is greater than function g(x)

( since 3>2 )

Hence, we get function f(x) is more steeper.

Answer 2

B. Function g has slope 3 which makes it steeper

EXPLANATION

The function f(x) has equation:

3x-y=6

We slope for y to get:

-y=-3x+6

y=3x-6

The slope of this function is 3.

The function g(x) passes through (-2,1) and (0,5).

The slope is

`m = (y_2-y_1)/(x_2-x_1)`

`m = (5- 1)/(0 - - 2)`

`m = (4)/(2) = 2`

Function g has slope 3. Hence it is steeper.