Question

A company produces and sells widgets and gizmos. In January the company sold 350 items for a total of $9,000. If each widget sold for $35, and each gizmo sold for $22, how many of each item did the company sell? Let x1 = the number of widgets sold and x2 = the number of gizmos sold.

Write an equation relating the number of each item sold to the total number sold: x1 + x2 =

Answer 1

x1 + x2 = 350

Explanation:

The total number of items sold is the sum of the number of widgets sold and the number of gizmos sold:

(widgets sold) + (gizmos sold) = total items sold

We are supposed to represent widgets sold using x1, and gizmos sold using x2. The total number of items sold is given in the problem statement as 350. Substituting these values into the above equation, we get the equation you're looking for:

x1 + x2 = 350

Answer 2

The company sold 100 widgets and 250 gizmos.

Explanation:

Let
`x_1` be the number of widgets sold and
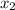`x_2` be the number of gizmos sold.

We are told that the company sold 350 items. We can represent this information in an equation as:

`x_1+x_2=350...(1)`

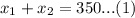
We have been given that a each widget sold for $35 and each gizmo sold for $22. The company sold 350 items for a total of $9,000.

We can represent this information in an equation as:

`35x_1+22x_2=9,000...(2)`

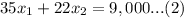
From equation (1), we will get:

`x_2=350-x_1`

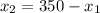
Substitute this value in equation (2):

`35x_1+22(350-x_1)=9,000`

`35x_1+7,700-22x_1=9,000`

`13x_1+7,700=9,000`

`13x_1+7,700-7,700=9,000-7,700`

`13x_1=1,300`

`(13x_1)/(13)=(1,300)/(13)`

`x_1=100`

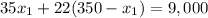
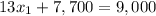
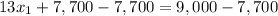
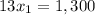
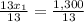
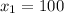
Therefore, the company sold 100 widgets.

Substitute
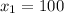`x_1=100` in equation (1):

`100+x_2=350`

`100-100+x_2=350-100`

`x_2=250`

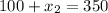
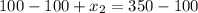
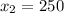
Therefore, the company sold 250 gizmos.