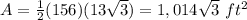Answer:
The area of the hexagon is
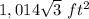
Explanation:
we know that
The area of a regular hexagon is equal to
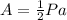
where
P is the perimeter
a is the apothem
Find the length side of the hexagon
Let
b-----> the length side of the hexagon
Remember that
The formula to calculate the length side given the apothem is equal to
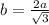
we have
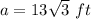
substitute
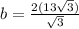
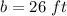
Find the perimeter P
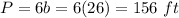
Find the area of the hexagon