Answer:
The correct answer is option B.
Explanation:
The given rational expression is:
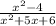
Factor the numerator and the denominator:
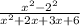
Factor the numerator using difference of two squares and the denominator using factorization by grouping.

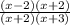
This function is defined if and only if the denominator is not zero.
That is: (x+3)(x+2)≠0.
x≠-2,x≠-3
We simplify now to obtain:
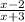
The correct choice is the second option.