Question

A system of equations consists of a line s of the equation y = x - 5 that is graphed in orange, and a line t that passes through the points (0, 2) and (8, -4). The equation of line t is y = −3 4 x + 2. What is the solution to this system of linear equations?

Answer 1

`x = 4`

and

`y = - 1`

EXPLANATION

Line s has equation:

y=x-5

And line t has equation:

`y = - (3)/(4)x + 2`

We equate the two equations to get:

`x - 5 = - (3)/(4) x + 2`

Multiply through by 4

`4x - 20 = - (3)/(4) x * 4 + 2 * 4`

`4x - 20 = - 3 x + 8`

`4x + 3x = 8 + 20`

7x=28

`x = (28)/(7) = 4`

`y = 4 - 5 = - 1`

Answer 2

(4, -1) is the solution of the system of equations.

Explanation:

A system of equations consists of a line y = x - 5 and a line passing through two points (0, 2) and (8, -4)

And the equation of that passes through these points will be
`y=-(3)/(4)x+2`

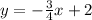
Now we have to find the solution of the system of linear equations.

By equating both the equations

x - 5 =
`-(3)/(4)x+2`

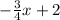
Now we multiply this equation by 4

4(x - 5) = -3x + 4×2

4x - 20 = -3x + 8

4x + 3x = 8 + 20

7x = 28

x = 4

Now we put x = 4 in the equation y = x - 5

y = 4 -5

y = -1

Therefore, (4, -1) is the solution of the system of equations.