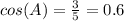Question

Find cos(A). reduce the ratio if necessary.

Answer 1

Final answer is
`\cos\left(A\right)=(3)/(5)`.

Explanation:

Using given information in the picture, we need ot find the missing value of Cos(A).

Apply formula of cosine function which is :

`\cos\left(A\right)=(Adjacent)/(Hypotenuse)`

`\cos\left(A\right)=(30)/(50)`

`\cos\left(A\right)=(3)/(5)`

Hence final answer is
`\cos\left(A\right)=(3)/(5)`.

Answer 2

`cos(A) =(3)/(5)=0.6`

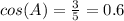
Explanation:

By definition the cosine of an angle is the quotient between the side adjacent to the angle and the hypotenuse.

In other words:

`cos (A) = (adjacent)/(hypotenuse)`

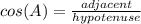
In this triangle the length of the side adjacent to the angle A is 30, and the length of the hypotenuse is 50

So:

`cos(A) = (30)/(50)`

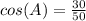
Simplifying we have that:

`cos(A) = (3)/(5)=0.6`