Question

What is the difference between a sequence and a series? What is the difference between a geometric and an arithmetic sequence?

Answer 1

Sequence: ordered list of numbers

Series: sum of the terms of a sequence

Arithmetic sequence: the difference between the terms is constant

Geometric Sequence: the ratio between the terms is constant

Explanation:

The difference between a series and a sequence is that a sequence is a list of numbers that follow a pattern or rule.

For example

1, 3, 5, 7, 9...

`a_n = 1 +2(n-1)`

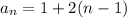
On the other hand, a series is the sum of the terms of a sequence.

1 + 3 + 5 + 7 + 9 + ...+ n

`\sum_(n=1)1 +2 (n-1)`

----------------------------------------------------------------------------------

The difference between an arithmetic sequence and a geometric sequence is that:

for the arithmetic sequences the subtraction of:

`a_n - a_(n-1) = d`

Where d is a constant called difference..

In the Arithmetic sequence the difference between the terms is constant

For the geometric sequences, it is satisfied that the quotient between two consecutive terms is:

`(a_(n-1))/(a_n) = r`

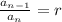
Where r is a constant value called common ratio

In geometric Sequence the ratio between the terms is constant