Question

Identify the correct trigonometry formula do you use to solve for the given angle

Answer 1

The correct trigonometry formula
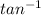`tan^(-1)` (71°) . Therefore ,
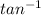`tan^(-1)`(71°) is correct .

The correct trigonometry formula to use to solve for the given angle is the tangent formula.

This is because you are given the side opposite to the angle (48) and the side adjacent to the angle (34), and you need to solve for the angle itself (71°).

The tangent formula is:

tan(angle) = opposite / adjacent

In this case, you would have:

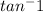`tan^-1` = 48 / 34

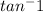`tan^-1` = 0. 708333 degree

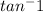`tan^-1` = 0.71 degree

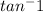`tan^-1` (0.71)

= 35.3112 degree.

Therefore, the correct answer is tan(71°).

Answer 2

`?=\tan^(-1)\left(0.71\right)` degree

Final answer is
`?=35` degree.

Explanation:

Using given information in the picture, we need to find the missing value of angle "?"

Apply formula of tangent function which is :

`\tan\left(\theta\right)=(opposite)/(adjacent)`

`\tan\left(?^o\right)=(34)/(48)`

`\tan\left(?^o\right)=0.70833333`

`?=\tan^(-1)\left(0.70833333\right)` degree

`?=\tan^(-1)\left(0.71\right)` degree

`?=35.311213439633198288773274209433` degree

Hence final answer is
`?=35` degree.