Question

The first steps in determining the perimeter of triangle ABC are shown.

To the nearest whole unit, what is the perimeter of triangle ABC?

Answer 1

14 units

Explanation:

.

Answer 2

Answer:
`P=14units`

Explanation:

The perimeter of a triangle is the sum of the lenghts of its sides.

Given the triangle ABC , its perimeter will be:

`P=AB+BC+CA`

Then, you know that the lenghts of the sids of the triangle ABC are:

`AB=3units\\BC=5units\\CA=√((3)^2+(-5)^2)=√(9+25)=√(34)=5.83units`

Therefore, to find the perimeter of this triangle, you need to substitute these lengthts into the formula
`P=AB+BC+CA`.

So, the perimeter of the triangle ABC is:

`P=3units+5units+5.83units=13.83units`

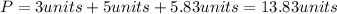
To the nearest whole unit is:

`P=14units`