Hello!
The answer is:
a) Her reasoning is incorrect, she applied a wrong operation, the way to simplify the expression was using the square root property. If we want to extract a number of a square root, we must square that number first in order not to modify the expression.
b) We have that:
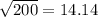
and rounding to the nearest tenth, we have that:
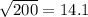
Why?
To solve the problem, we need to remember the following property of square roots:
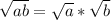
We are given the expression:
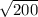
We can rewrite it by the following way:
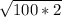
Now, applying the square root property we have:
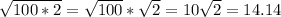
Therefore,
a) Her reasoning was wrong, she applied a wrong operation, the way to simplify the expression was using the square root property. If we want to extract a number of a square root, we must square that number first in order not to modify the expression.
b) We have that:
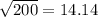
and rounding to the nearest tenth, we have that:
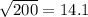
Have a nice day!