Hello!
The answers are:
C)
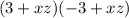
D)
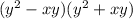
F)
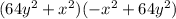
Why?
To know which of the products results in a difference of square, we need to remember the difference of squares from:
The difference of squares form is:
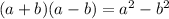
So, discarding each of the given options in order to find which products result in a difference of squares, we have:
A)
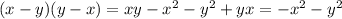
So, the obtained expression is not a difference of squares.
B)

So, the obtained expression is not a difference of squares.
C)
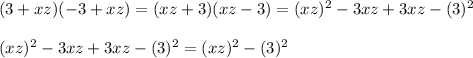
So, the obtained expression is a difference of squares since it matches with the form of the difference of squares.
D)
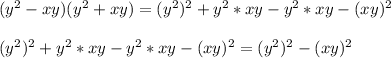
So, the obtained expression is a difference of squares since it matches with the form of the difference of squares.
E)
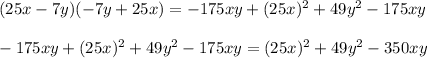
So, the obtained expression is not a difference of squares
F)
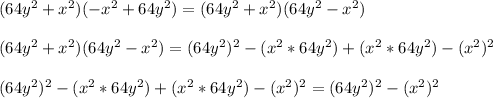
So, the obtained expression is a difference of squares since it matches with the form of the difference of squares.
Hence, the products that result in a difference of squares are:
C)
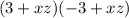
D)
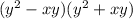
F)
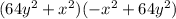
Have a nice day!