Question

The Pickering nuclear power plant has a power rating of 3100 MW.

How much output energy can the generating station produce in one day. Express your answer in Mj

Answer 1

`2.68\cdot 10^8 MJ`

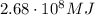
Step-by-step explanation:

The power is related to the energy by

`P=(E)/(t)`

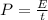
where

P is the power

E is the energy

t is the time elapsed

The power of this nuclear power planet is

`P=3100 MW = 3.1\cdot 10^9 W`

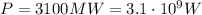
The time we are considering is 1 day, which is

`t = 1 d = 86400 s`

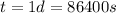
So we can re-arrange the previous equation to find the energy produced by the power plant in one day:

`E=Pt =(3.1\cdot 10^9 W)(86400 s)=2.68\cdot 10^(14) J=2.68\cdot 10^8 MJ`