Question

Which statements are true about the fully simplified product of (b-2c)(-3b c) ?

Select two options.
( 1 )The simplified product has 2 terms.
( 2 )The simplified product has 4 terms.
( 3 )The simplified product has a degree of 2.
( 4 )The simplified product has a degree of 3.
( 5 )The simplified product has a degree of 4.
( 6 )The simplified product, in standard form, has exactly 2 negative terms.

Answer 1

( 3 )The simplified product has a degree of 2.

Explanation:

`(b-2c)(-3b+c)`

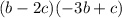
Multiply the parenthesis using FOIL method

multiply b inside the second parenthesis

`b(-3b+c)= -3b^2 +bc`

`-2c(-3b+c)= 6bc -2c^2`

`(-3b^2 +bc+6bc -2c^2)`

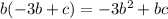
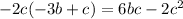
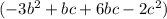
Combine like terms

`-3b^2 +7bc -2c^2`

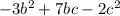
Simplified product has 3 terms, and the degree of 2 because we have b^2

and c^2