Question

The graph shows the total cost (y) of producing x motorbike engines.

Complete the following sentences based on the graph.

The equation of the line is y = .

The total cost of producing 50 engines is .
option 1
0.2x+2
0.25x+2
0.4x+2
1.2x+2

option 2
$12,250
$14,750
$14,500
$15,000

Answer 1

1. B

2. C

Explanation:

☺☻

Answer 2

1) Second option:
`y=0.25x+2`

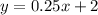
2) Third option: $14,500

Explanation:

1) The equation of the line in Slope-intercept form is:

`y=mx+b`

Where m is the slope and b is the y-intercept.

You know the point (20,7) of the line and you can observe in the graph that the y-intercept is:

`b=2`

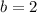
Then, you can substitute these values into the equation
`y=mx+b`

and solve for the slope "m":

`7=m(20)+2\\\\7-2=20m\\\\m=(5)/(20)\\\\m=0.25`

Therefore, the equation of this line is:

`y=0.25x+2`

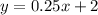
2) To calculate the total cost of producing 50 engines, you need to substitute
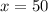`x=50` into the equation of the line
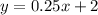`y=0.25x+2`. Then you get:

`y=0.25(50)+2`

`y=0.25x+2`

`y=14.5`

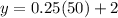
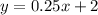
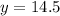
Since the y-axis represents the total cost "y" in thousands of dollar, then the total cost of producing 50 engines is:

$14,500