Answer:
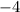
Explanation:
The given logarithmic equation is:
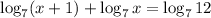
Recall and apply product rule of logarithms.
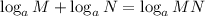
We apply this property to the left side of the equation to get;

We take the antilogarithm of both sides to get:
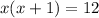
We expand to obtain:

We rewrite in the standard quadratic form:
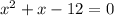
We factor to obtain:
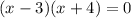
Either
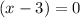 or
or
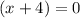
Either
 or
or
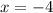
But the domain is
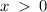 .
.
Hence
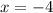 is an extraneous solution.
is an extraneous solution.