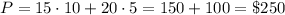Question

Lisa has an online jewelry shop where she sells earrings and necklaces. SHe sells earrings for $30 and necklaces for $40. It takes half an hour to make a pair of earrings and 1 hour to make a necklace. Lisa only has 10 hours a week to make jewelry. In addition, she only has enough materials to make 15 total jewelry items per week. She makes a profit of $15 on each pair of earrings and $20 on each necklace. How many pairs of earrings and necklaces should Lisa make each week in order to maximize her profit, assuming she sells all her jewelry?

Answer 1

10 pairs of earrings and 5 necklaces (the maximum profit will be $250)

Explanation:

Let x be the number of earrings and y be the number of necklaces Lisa makes.

1. Lisa only has enough materials to make 15 total jewelry items per week, then

`x+y\le 15.`

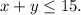
2. It takes half an hour to make a pair of earrings, so it takes her
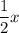`(1)/(2)x` hours to make x earrings. It takes her 1 hour to make a necklace, so it takes her y hours to make y necklaces. Lisa only has 10 hours a week to make jewelry, thus

`(x)/(2)+y\le 10`

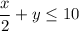
3. Lisa makes a profit of $15 on each pair of earrings and $20 on each necklace. In total her profit is

`P=15x+20y.`

You have to find the maximum value of the function
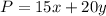`P=15x+20y` with respect to inequalities

`x+y\le 15\\ \\(x)/(2)+y\le 10`

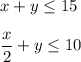
Draw the solution set on the coordinate plane (see attached diagram). The maximum value of the efunction P is at point (10,5) and is

`P=15\cdot 10+20\cdot 5=150+100=\$250`