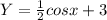Answer: Last Option
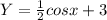
Explanation:
If the graph of the function
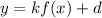 represents the transformations made to the graph of
represents the transformations made to the graph of
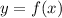 then, by definition:
then, by definition:
If
 then the graph is compressed vertically by a factor k.
then the graph is compressed vertically by a factor k.
If
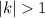 then the graph is stretched vertically by a factor k
then the graph is stretched vertically by a factor k
If
 then the graph is reflected on the x axis.
then the graph is reflected on the x axis.
If
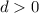 the graph moves vertically upwards d units.
the graph moves vertically upwards d units.
If
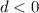 the graph moves vertically down d units.
the graph moves vertically down d units.
In this problem we have the function

And we know that The graph of
 is transformed with a vertical compression by a factor of 1/2 and a translation 3 units up
is transformed with a vertical compression by a factor of 1/2 and a translation 3 units up
therefore it is true that
 and
and
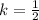 and
and
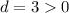
Therefore the new equation is: