Question

If a 20 kg artillery shell is launched vertically with a velocity of 37 m/s, how high in meters does it rise? Use the acceleration due to gravity as 9.8 m/s2.

or-
how do you calculate projectile motion? What are the formulas?

Answer 1

1. 69.8 m

The vertical motion of the shell is a uniformly accelerated motion, with constant acceleration
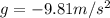`g=-9.81 m/s^2` towards the ground (acceleration due to gravity).

At the point of maximum height, the velocity of the projectile is zero:

v = 0

So we can find the maximum height by using the equation:

`v^2 -u^2 = 2gd`

where

u = 37 m/s is the initial velocity

d is the maximum heigth

Solving for d,

`d=(v^2-u^2)/(2g)=(0^2-(37 m/s)^2)/(2(-9.81 m/s^2))=69.8 m`

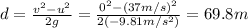
2)

A projectile motion consists of two separate motions:

- A uniform motion along the x-direction, with constant velocity given by

`v_x = v_0 cos \theta`

where
`v_0` is the initial velocity, and
`\theta` the angle of launch

- A unformly accelerated motion along the y-direction, with initial velocity

`v_y = v_0 sin \theta`

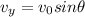
and constant acceleration

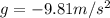`g=-9.81 m/s^2` (acceleration due to gravity) towards the ground.

The horizontal position of the projectile at time t is given by

`x(t) = v_x t`

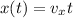
while the vertical position is given by

`y(t) = y_0 + v_0 sin \theta t + (1)/(2)gt^2`

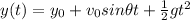
where
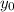`y_0` is the initial height of the projectile.