For this case we have that by definition:
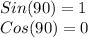
Now, the tangent of 90 is given by:
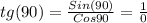
Thus, it is observed that the tangent of 90 degrees is not defined. Is obtained ∞.
Similarly:
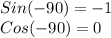
Now, the tangent of -90 is given by:
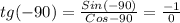
Thus, it is observed that the tangent of -90 degrees is not defined.
Answer:
False