Question

`\boxed{\boxed{ \begin{array}{}\large\tt The \\ \tt \large Distance \: Formula \: \\ \large \tt and \\ \large\tt \: Coordinate \: Proof \end{array}}}`

Direction: Find the distance between each pair of points on the coordinate plane and write the solution.


1. A(3, 8) and B(3, -2)

2. O(5, -2) and K(7, -2)

3. L(4, -4) and M(-4, 6)

4. P(5, 1) and C(2, 3)

5. Q(-10, 9) and R(-2, 3)


`\boxed{\boxed{ \begin{array}{}\large\tt Nonsense + Useless \\ \large \tt= Report! \end{array}}}`
​

Answer 1

Distance formula

`\boxed{\sf √((x_2-x_1)^2+(y_2-y_1)^2)}`

Now

#1

`\\ \tt\Rrightarrow AB=√((3-3)^2+(-2-8)^2)=√(100)=10units`

#2

`\\ \tt\Rrightarrow OK=√((5-7)^2+(-2+2)^2)=√(4)=2units`

#3

`\\ \tt\Rrightarrow LM=√((-4-4)^2+(6+4)^2)=√(64+100)=√(164)\approx 13units`

#4

`\\ \tt\Rrightarrow PC=√((5-2)^2+(1-3)^2)=√(9+4)=√(13)=3.2units`

#5

`\\ \tt\Rrightarrow QR=√((-2+10)^2+(3-9)^2)=√(64+36)=√(100)=10units`

Answer 2

Answer of all given questions are given below :

• 1) AB = 10 units
• 2) OK = 2 units
• 3) LM = 2√41 units
• 4) PC ≈ 3.6 units
• 5) QR = 10 units

Step-by-step Step-by-step explanation:

Here's the required formula to find distance between points :

`\star{\small{\underline{\boxed{\sf{\red{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}}}`

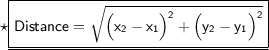
According to this formula, we'll solve all the given questions and find the distance between points.

1. A(3, 8) and B(3, -2)

Substituting all the given values in the formula to find the distance between points:

`{\implies{\small{\sf{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}`

`{\implies{\small{\sf{AB = \sqrt{\Big(3 - 3 \Big)^(2) + \Big( - 2 - 8 \Big)^(2)}}}}}`

`{\implies{\small{\sf{AB = \sqrt{\Big(0\Big)^(2) + \Big( - 10 \Big)^(2)}}}}}`

`{\implies{\small{\sf{AB = √(\Big(0 * 0\Big) + \Big( - 10 * - 10 \Big))}}}}`

`{\implies{\small{\sf{AB = √(\big(0 + 100\big))}}}}`

`{\implies{\small{\sf{AB = √(100)}}}}`

`{\implies{\sf{\underline{\underline{\purple{AB = 10}}}}}}`

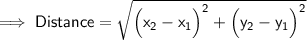
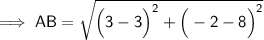
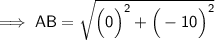
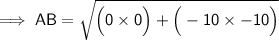
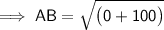
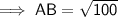
Hence, the distance between points AB is 10 units..

`\begin{gathered}\end{gathered}`

2. O(5, -2) and K(7, -2)

Substituting all the given values in the formula to find the distance between points:

`{\longrightarrow{\small{\sf{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}`

`{\longrightarrow{\small{\sf{OK = \sqrt{\Big(7 - 5\Big)^(2) + \Big( - 2 + 2 \Big)^(2)}}}}}`

`{\longrightarrow{\small{\sf{OK = \sqrt{\Big(2\Big)^(2) + \Big(0 \Big)^(2)}}}}}`

`{\longrightarrow{\small{\sf{OK = √(\Big(2 * 2\Big) + \Big(0 * 0 \Big))}}}}`

`{\longrightarrow{\small{\sf{OK = √(\big(4 + 0 \big))}}}}`

`{\longrightarrow{\small{\sf{OK = √(4)}}}}`

`{\longrightarrow{\sf{\underline{\underline{\pink{OK = 2}}}}}}`

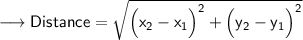
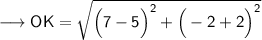
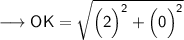
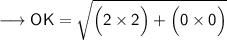
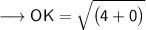
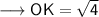
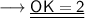
Hence, the distance between points OK is 2 units.

`\begin{gathered}\end{gathered}`

3. L(4, -4) and M(-4, 6)

Substituting all the given values in the formula to find the distance between points:

`{\longmapsto{\small{\sf{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}`

`{\longmapsto{\small{\sf{LM = \sqrt{\Big( - 4 - 4\Big)^(2) + \Big( 6 + 4 \Big)^(2)}}}}}`

`{\longmapsto{\small{\sf{LM = \sqrt{\Big( - 8\Big)^(2) + \Big(10 \Big)^(2)}}}}}`

`{\longmapsto{\small{\sf{LM = √(\Big( - 8 * - 8\Big) + \Big(10 * 10\Big))}}}}`

`{\longmapsto{\small{\sf{LM = √(\big( 64 + 100\big))}}}}`

`{\longmapsto{\small{\sf{LM = √(164)}}}}`

`{\longmapsto{\sf{\underline{\underline{\orange{LM = 2 √(41) }}}}}}`

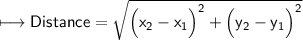
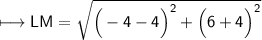
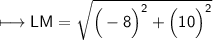
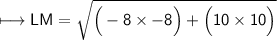
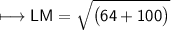
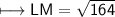
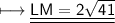
Hence, the distance between points LM is 2√41 units.

`\begin{gathered}\end{gathered}`

4. P(5, 1) and C(2, 3)

Substituting all the given values in the formula to find the distance between points:

`{\dashrightarrow{\small{\sf{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}`

`{\dashrightarrow{\small{\sf{PC = \sqrt{\Big(2 - 5 \Big)^(2) + \Big(3 - 1 \Big)^(2)}}}}}`

`{\dashrightarrow{\small{\sf{PC = \sqrt{\Big( - 3\Big)^(2) + \Big(2\Big)^(2)}}}}}`

`{\dashrightarrow{\small{\sf{PC = √(\Big( - 3 * - 3\Big) + \Big(2 * 2\Big))}}}}`

`{\dashrightarrow{\small{\sf{PC = √(\big( 9 + 4\big))}}}}`

`{\dashrightarrow{\small{\sf{PC = √(13)}}}}`

`{\dashrightarrow{\sf{\underline{\underline{\green{PC \approx 3.6}}}}}}`

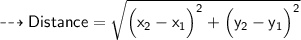
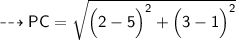
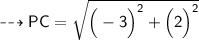
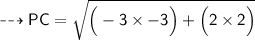
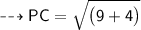
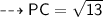
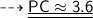
Hence, the distance between points PC is 3.6 units.

`\begin{gathered}\end{gathered}`

5. Q(-10, 9) and R(-2, 3)

Substituting all the given values in the formula to find the distance between points:

`{\twoheadrightarrow{\small{\sf{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}`

`{\twoheadrightarrow{\small{\sf{QR = \sqrt{\Big( - 2 + 10 \Big)^(2) + \Big(3 - 9 \Big)^(2)}}}}}`

`{\twoheadrightarrow{\small{\sf{QR = \sqrt{\Big( 8 \Big)^(2) + \Big( - 6\Big)^(2)}}}}}`

`{\twoheadrightarrow{\small{\sf{QR = √(\Big( 8 * 8 \Big)+ \Big( - 6 * - 6\Big))}}}}`

`{\twoheadrightarrow{\small{\sf{QR = √(\big(64 + 36\big))}}}}`

`{\twoheadrightarrow{\small{\sf{QR = √(100)}}}}`

`{\twoheadrightarrow{\sf{\underline{\underline{\blue{QR = 10}}}}}}`

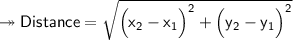
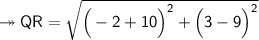
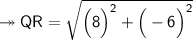
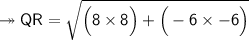
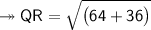
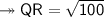
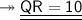
Hence, the distance between points QR is 10 units.

`\rule{300}{2.5}`