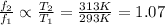Question

By what factor does the peak frequency change if the celsius temperature of an object is doubled from 20.0 ∘c to 40.0 ∘c?

Answer 1

it increases by a factor 1.07

Step-by-step explanation:

The peak wavelength of an object is given by Wien's displacement law:

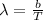`\lambda=(b)/(T)` (1)

where

b is the Wien's displacement constant

T is the temperature (in Kelvins) of the object

given the relationship between frequency and wavelength of an electromagnetic wave:

`f=(c)/(\lambda)`

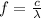
where c is the speed of light, we can rewrite (1) as

`(c)/(f)=(b)/(T)\\f=(Tc)/(b)`

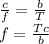
So the peak frequency is directly proportional to the temperature in Kelvin.

In this problem, the temperature of the object changes from

`T_1 = 20.0^(\circ)+273=293 K`

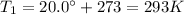
to

`T_2 = 40.0^(\circ)+273 = 313 K`

so the peak frequency changes by a factor

`(f_2)/(f_1) \propto (T_2)/(T_1)=(313 K)/(293 K)=1.07`