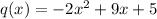Question

What is the quotient of the synthetic division problem below written in polynomial form?

Answer 1

-2x^2 + 21x + 41 with a remainder of 108 (Answer A)

Explanation:

Let's perform the indicated synthetic division:

3 ) -2 15 -22 -15

6 63 123

-----------------------------

-2 21 41 108

We take the first three coefficients of these results and use them to write a polynomial which represents the quotient:

-2x^2 + 21x + 41 with a remainder of 108 (Answer A)

Answer 2

D.
`q(x) = - 2 {x}^(2) + 9x +5`

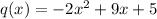
EXPLANATION

We perform the synthetic division to get:

-2 15 -22 -15

3| -6 27 15

-2 9 5 0

From the synthetic division problem;

The coefficient of the quotient are the first three numbers.

-2, 9, 5

The last number 0 is the remainder

Since the coefficient of the quotient are three, it means the polynomial having 2 as the highest degree.

Therefore the quotient is:

`q(x) = - 2 {x}^(2) + 9x +5`